This post is in a series on doing machine learning with unbalanced datasets. This post focuses on the evaluation aspect in particular. For background, please see the setup post.
When we’re evaluating the performance of models on an unbalanced dataset, what should the makeup of the test set be? This post digs into this question.
Table of Contents
%run 2021-05-01-prep-for-experiements-on-unbalanced-datasets.ipynb
Classes:
['cats', 'dogs']
There are a total of 5000 cat images in the entire dataset.
There are a total of 5000 dog images in the entire dataset.
Train Model
OK. Our first experiment we’ll make a couple train datasets. One option is to have a balanced dataset, the other is to allow it to be unbalanced to match the “real world”. Let’s see which one produces better results.
cat_list_train, cat_list_val, cat_list_test_balanced, cat_list_test_unbalanced = subset_dataset(cat_list_ds, [1000, 1000, 1500, 1500])
dog_list_train, dog_list_val, dog_list_test_balanced, dog_list_test_unbalanced = subset_dataset(dog_list_ds, [1000, 100, 1500, 150])
train_ds = prepare_dataset(cat_list_train, dog_list_train)
val_ds = prepare_dataset(cat_list_val, dog_list_val)
test_ds_balanced = prepare_dataset(cat_list_test_balanced, dog_list_test_balanced)
test_ds_unbalanced = prepare_dataset(cat_list_test_unbalanced, dog_list_test_unbalanced)
Great. Now let’s train the models. We have two. One that likes cats more than dogs and one that likes dogs more than cats.
cat_weights = {0:2, 1:1}
model_cat = get_model()
model_cat.compile(optimizer='adam', loss='binary_crossentropy', metrics=all_metrics)
history_cat = model_cat.fit(train_ds, epochs=NUM_EPOCHS, validation_data=val_ds, class_weight=cat_weights)
Epoch 1/20
63/63 [==============================] - 12s 136ms/step - loss: 1.6739 - tp: 93.8438 - fp: 89.8906 - tn: 409.1562 - fn: 446.1094 - accuracy: 0.4793 - precision: 0.5059 - recall: 0.2298 - val_loss: 0.3773 - val_tp: 0.0000e+00 - val_fp: 0.0000e+00 - val_tn: 1000.0000 - val_fn: 100.0000 - val_accuracy: 0.9091 - val_precision: 0.0000e+00 - val_recall: 0.0000e+00
Epoch 2/20
63/63 [==============================] - 6s 102ms/step - loss: 1.0291 - tp: 1.5000 - fp: 0.4844 - tn: 498.5625 - fn: 538.4531 - accuracy: 0.4762 - precision: 0.2143 - recall: 0.0015 - val_loss: 0.3244 - val_tp: 0.0000e+00 - val_fp: 0.0000e+00 - val_tn: 1000.0000 - val_fn: 100.0000 - val_accuracy: 0.9091 - val_precision: 0.0000e+00 - val_recall: 0.0000e+00
Epoch 3/20
63/63 [==============================] - 6s 101ms/step - loss: 1.0926 - tp: 0.2188 - fp: 0.2812 - tn: 498.7656 - fn: 539.7344 - accuracy: 0.4756 - precision: 0.0729 - recall: 2.2158e-04 - val_loss: 0.3490 - val_tp: 0.0000e+00 - val_fp: 0.0000e+00 - val_tn: 1000.0000 - val_fn: 100.0000 - val_accuracy: 0.9091 - val_precision: 0.0000e+00 - val_recall: 0.0000e+00 0.1000 - fp: 0.1667 - tn: 466.5500 - fn: 509.1833 - accuracy: 0.4743 - precision: 0.0444 - recall: 1.0302e
Epoch 4/20
63/63 [==============================] - 6s 103ms/step - loss: 1.0051 - tp: 3.3594 - fp: 0.7500 - tn: 498.2969 - fn: 536.5938 - accuracy: 0.4775 - precision: 0.7893 - recall: 0.0044 - val_loss: 0.3781 - val_tp: 1.0000 - val_fp: 7.0000 - val_tn: 993.0000 - val_fn: 99.0000 - val_accuracy: 0.9036 - val_precision: 0.1250 - val_recall: 0.0100
Epoch 5/20
63/63 [==============================] - 6s 101ms/step - loss: 0.9658 - tp: 27.1875 - fp: 10.9531 - tn: 488.0938 - fn: 512.7656 - accuracy: 0.4876 - precision: 0.6462 - recall: 0.0378 - val_loss: 0.3864 - val_tp: 3.0000 - val_fp: 4.0000 - val_tn: 996.0000 - val_fn: 97.0000 - val_accuracy: 0.9082 - val_precision: 0.4286 - val_recall: 0.0300
Epoch 6/20
63/63 [==============================] - 6s 102ms/step - loss: 0.9325 - tp: 53.0469 - fp: 17.1719 - tn: 481.8750 - fn: 486.9062 - accuracy: 0.5036 - precision: 0.7886 - recall: 0.0781 - val_loss: 0.3151 - val_tp: 4.0000 - val_fp: 2.0000 - val_tn: 998.0000 - val_fn: 96.0000 - val_accuracy: 0.9109 - val_precision: 0.6667 - val_recall: 0.0400 12.2593 - fp: 4.2593 - tn: 207.2593 - fn: 224.2
Epoch 7/20
63/63 [==============================] - 6s 102ms/step - loss: 0.9403 - tp: 99.5000 - fp: 36.5312 - tn: 462.5156 - fn: 440.4531 - accuracy: 0.5310 - precision: 0.7655 - recall: 0.1643 - val_loss: 0.3633 - val_tp: 8.0000 - val_fp: 11.0000 - val_tn: 989.0000 - val_fn: 92.0000 - val_accuracy: 0.9064 - val_precision: 0.4211 - val_recall: 0.0800
Epoch 8/20
63/63 [==============================] - 6s 101ms/step - loss: 0.8855 - tp: 128.5938 - fp: 26.9062 - tn: 472.1406 - fn: 411.3594 - accuracy: 0.5622 - precision: 0.8535 - recall: 0.2054 - val_loss: 0.3632 - val_tp: 23.0000 - val_fp: 30.0000 - val_tn: 970.0000 - val_fn: 77.0000 - val_accuracy: 0.9027 - val_precision: 0.4340 - val_recall: 0.2300
Epoch 9/20
63/63 [==============================] - 6s 102ms/step - loss: 0.8649 - tp: 197.7969 - fp: 52.0000 - tn: 447.0469 - fn: 342.1562 - accuracy: 0.6036 - precision: 0.8166 - recall: 0.3249 - val_loss: 0.3294 - val_tp: 19.0000 - val_fp: 18.0000 - val_tn: 982.0000 - val_fn: 81.0000 - val_accuracy: 0.9100 - val_precision: 0.5135 - val_recall: 0.1900
Epoch 10/20
63/63 [==============================] - 6s 101ms/step - loss: 0.8330 - tp: 232.6562 - fp: 53.4688 - tn: 445.5781 - fn: 307.2969 - accuracy: 0.6407 - precision: 0.8441 - recall: 0.3971 - val_loss: 0.3074 - val_tp: 27.0000 - val_fp: 20.0000 - val_tn: 980.0000 - val_fn: 73.0000 - val_accuracy: 0.9155 - val_precision: 0.5745 - val_recall: 0.2700
Epoch 11/20
63/63 [==============================] - 6s 102ms/step - loss: 0.7708 - tp: 267.2344 - fp: 57.1094 - tn: 441.9375 - fn: 272.7188 - accuracy: 0.6619 - precision: 0.8472 - recall: 0.4464 - val_loss: 0.3283 - val_tp: 33.0000 - val_fp: 35.0000 - val_tn: 965.0000 - val_fn: 67.0000 - val_accuracy: 0.9073 - val_precision: 0.4853 - val_recall: 0.3300
Epoch 12/20
63/63 [==============================] - 6s 102ms/step - loss: 0.7532 - tp: 257.2500 - fp: 53.2656 - tn: 445.7812 - fn: 282.7031 - accuracy: 0.6576 - precision: 0.8504 - recall: 0.4296 - val_loss: 0.2757 - val_tp: 26.0000 - val_fp: 18.0000 - val_tn: 982.0000 - val_fn: 74.0000 - val_accuracy: 0.9164 - val_precision: 0.5909 - val_recall: 0.2600
Epoch 13/20
63/63 [==============================] - 6s 102ms/step - loss: 0.7574 - tp: 263.6094 - fp: 51.3438 - tn: 447.7031 - fn: 276.3438 - accuracy: 0.6616 - precision: 0.8606 - recall: 0.4355 - val_loss: 0.3514 - val_tp: 45.0000 - val_fp: 88.0000 - val_tn: 912.0000 - val_fn: 55.0000 - val_accuracy: 0.8700 - val_precision: 0.3383 - val_recall: 0.4500
Epoch 14/20
63/63 [==============================] - 6s 102ms/step - loss: 0.6374 - tp: 325.6875 - fp: 50.2812 - tn: 448.7656 - fn: 214.2656 - accuracy: 0.7368 - precision: 0.8730 - recall: 0.5846 - val_loss: 0.3274 - val_tp: 48.0000 - val_fp: 81.0000 - val_tn: 919.0000 - val_fn: 52.0000 - val_accuracy: 0.8791 - val_precision: 0.3721 - val_recall: 0.480017 - fp: 46.6949 - tn: 412.3220 - fn: 199.8814 - accuracy: 0.7350 - precision: 0.8733 - recall
Epoch 15/20
63/63 [==============================] - 6s 102ms/step - loss: 0.6105 - tp: 348.7656 - fp: 50.8594 - tn: 448.1875 - fn: 191.1875 - accuracy: 0.7593 - precision: 0.8840 - recall: 0.6257 - val_loss: 0.3482 - val_tp: 49.0000 - val_fp: 91.0000 - val_tn: 909.0000 - val_fn: 51.0000 - val_accuracy: 0.8709 - val_precision: 0.3500 - val_recall: 0.4900
Epoch 16/20
63/63 [==============================] - 6s 101ms/step - loss: 0.5306 - tp: 368.2500 - fp: 50.0156 - tn: 449.0312 - fn: 171.7031 - accuracy: 0.7785 - precision: 0.8862 - recall: 0.6644 - val_loss: 0.3167 - val_tp: 45.0000 - val_fp: 70.0000 - val_tn: 930.0000 - val_fn: 55.0000 - val_accuracy: 0.8864 - val_precision: 0.3913 - val_recall: 0.4500
Epoch 17/20
63/63 [==============================] - 6s 102ms/step - loss: 0.5108 - tp: 380.3750 - fp: 42.6875 - tn: 456.3594 - fn: 159.5781 - accuracy: 0.7921 - precision: 0.9033 - recall: 0.6779 - val_loss: 0.3349 - val_tp: 49.0000 - val_fp: 88.0000 - val_tn: 912.0000 - val_fn: 51.0000 - val_accuracy: 0.8736 - val_precision: 0.3577 - val_recall: 0.4900
Epoch 18/20
63/63 [==============================] - 6s 102ms/step - loss: 0.4566 - tp: 400.2344 - fp: 30.5625 - tn: 468.4844 - fn: 139.7188 - accuracy: 0.8220 - precision: 0.9394 - recall: 0.7093 - val_loss: 0.4254 - val_tp: 56.0000 - val_fp: 161.0000 - val_tn: 839.0000 - val_fn: 44.0000 - val_accuracy: 0.8136 - val_precision: 0.2581 - val_recall: 0.5600
Epoch 19/20
63/63 [==============================] - 6s 101ms/step - loss: 0.4145 - tp: 416.8906 - fp: 37.2656 - tn: 461.7812 - fn: 123.0625 - accuracy: 0.8435 - precision: 0.9250 - recall: 0.7640 - val_loss: 0.3894 - val_tp: 55.0000 - val_fp: 144.0000 - val_tn: 856.0000 - val_fn: 45.0000 - val_accuracy: 0.8282 - val_precision: 0.2764 - val_recall: 0.5500
Epoch 20/20
63/63 [==============================] - 6s 101ms/step - loss: 0.4269 - tp: 424.6406 - fp: 31.3438 - tn: 467.7031 - fn: 115.3125 - accuracy: 0.8460 - precision: 0.9299 - recall: 0.7646 - val_loss: 0.4071 - val_tp: 53.0000 - val_fp: 125.0000 - val_tn: 875.0000 - val_fn: 47.0000 - val_accuracy: 0.8436 - val_precision: 0.2978 - val_recall: 0.5300
dog_weights = {0:1, 1:2}
model_dog = get_model()
model_dog.compile(optimizer='adam', loss='binary_crossentropy', metrics=all_metrics)
history_dog = model_dog.fit(train_ds, epochs=NUM_EPOCHS, validation_data=val_ds, class_weight=dog_weights)
Epoch 1/20
63/63 [==============================] - 9s 114ms/step - loss: 1.3437 - tp: 544.4062 - fp: 593.5781 - tn: 905.4688 - fn: 95.5469 - accuracy: 0.6928 - precision: 0.4609 - recall: 0.8004 - val_loss: 0.7637 - val_tp: 100.0000 - val_fp: 1000.0000 - val_tn: 0.0000e+00 - val_fn: 0.0000e+00 - val_accuracy: 0.0909 - val_precision: 0.0909 - val_recall: 1.0000
Epoch 2/20
63/63 [==============================] - 6s 102ms/step - loss: 0.9903 - tp: 539.9531 - fp: 499.0469 - tn: 0.0000e+00 - fn: 0.0000e+00 - accuracy: 0.5243 - precision: 0.5243 - recall: 1.0000 - val_loss: 0.7420 - val_tp: 100.0000 - val_fp: 958.0000 - val_tn: 42.0000 - val_fn: 0.0000e+00 - val_accuracy: 0.1291 - val_precision: 0.0945 - val_recall: 1.0000
Epoch 3/20
63/63 [==============================] - 6s 101ms/step - loss: 0.9745 - tp: 531.9688 - fp: 477.0000 - tn: 22.0469 - fn: 7.9844 - accuracy: 0.5377 - precision: 0.5322 - recall: 0.9827 - val_loss: 0.7959 - val_tp: 98.0000 - val_fp: 856.0000 - val_tn: 144.0000 - val_fn: 2.0000 - val_accuracy: 0.2200 - val_precision: 0.1027 - val_recall: 0.9800
Epoch 4/20
63/63 [==============================] - 6s 101ms/step - loss: 0.9430 - tp: 515.1406 - fp: 435.8125 - tn: 63.2344 - fn: 24.8125 - accuracy: 0.5584 - precision: 0.5451 - recall: 0.9541 - val_loss: 0.5574 - val_tp: 41.0000 - val_fp: 169.0000 - val_tn: 831.0000 - val_fn: 59.0000 - val_accuracy: 0.7927 - val_precision: 0.1952 - val_recall: 0.4100
Epoch 5/20
63/63 [==============================] - 7s 103ms/step - loss: 1.0024 - tp: 491.6875 - fp: 433.0625 - tn: 65.9844 - fn: 48.2656 - accuracy: 0.5415 - precision: 0.5468 - recall: 0.8426 - val_loss: 0.6341 - val_tp: 51.0000 - val_fp: 385.0000 - val_tn: 615.0000 - val_fn: 49.0000 - val_accuracy: 0.6055 - val_precision: 0.1170 - val_recall: 0.5100
Epoch 6/20
63/63 [==============================] - 6s 102ms/step - loss: 0.9782 - tp: 495.4844 - fp: 400.0000 - tn: 99.0469 - fn: 44.4688 - accuracy: 0.5803 - precision: 0.5709 - recall: 0.8707 - val_loss: 0.7442 - val_tp: 87.0000 - val_fp: 676.0000 - val_tn: 324.0000 - val_fn: 13.0000 - val_accuracy: 0.3736 - val_precision: 0.1140 - val_recall: 0.8700
Epoch 7/20
63/63 [==============================] - 6s 102ms/step - loss: 0.8820 - tp: 502.7031 - fp: 388.1250 - tn: 110.9219 - fn: 37.2500 - accuracy: 0.6017 - precision: 0.5769 - recall: 0.9161 - val_loss: 0.7042 - val_tp: 82.0000 - val_fp: 545.0000 - val_tn: 455.0000 - val_fn: 18.0000 - val_accuracy: 0.4882 - val_precision: 0.1308 - val_recall: 0.8200
Epoch 8/20
63/63 [==============================] - 6s 102ms/step - loss: 0.8579 - tp: 491.5156 - fp: 358.1406 - tn: 140.9062 - fn: 48.4375 - accuracy: 0.6194 - precision: 0.5920 - recall: 0.8963 - val_loss: 0.7233 - val_tp: 87.0000 - val_fp: 603.0000 - val_tn: 397.0000 - val_fn: 13.0000 - val_accuracy: 0.4400 - val_precision: 0.1261 - val_recall: 0.8700
Epoch 9/20
63/63 [==============================] - 6s 102ms/step - loss: 0.8500 - tp: 490.7188 - fp: 330.8906 - tn: 168.1562 - fn: 49.2344 - accuracy: 0.6408 - precision: 0.6073 - recall: 0.9002 - val_loss: 0.5494 - val_tp: 62.0000 - val_fp: 257.0000 - val_tn: 743.0000 - val_fn: 38.0000 - val_accuracy: 0.7318 - val_precision: 0.1944 - val_recall: 0.6200
Epoch 10/20
63/63 [==============================] - 6s 103ms/step - loss: 0.8489 - tp: 473.7812 - fp: 307.0312 - tn: 192.0156 - fn: 66.1719 - accuracy: 0.6428 - precision: 0.6217 - recall: 0.8380 - val_loss: 0.6553 - val_tp: 80.0000 - val_fp: 392.0000 - val_tn: 608.0000 - val_fn: 20.0000 - val_accuracy: 0.6255 - val_precision: 0.1695 - val_recall: 0.8000
Epoch 11/20
63/63 [==============================] - 6s 102ms/step - loss: 0.7848 - tp: 471.3594 - fp: 268.1406 - tn: 230.9062 - fn: 68.5938 - accuracy: 0.6779 - precision: 0.6496 - recall: 0.8493 - val_loss: 0.5144 - val_tp: 61.0000 - val_fp: 202.0000 - val_tn: 798.0000 - val_fn: 39.0000 - val_accuracy: 0.7809 - val_precision: 0.2319 - val_recall: 0.6100130.9394 - tn: 126.8788 - fn: 46.3030 - accuracy: 0.6803 - precision: 0.6647 - recall: 0.81 - ETA: 1s - loss: 0.8033 - tp: 247.2353 - fp: 135.6471 - tn: 130.0000 - fn: 47.11
Epoch 12/20
63/63 [==============================] - 6s 99ms/step - loss: 0.7556 - tp: 461.1094 - fp: 238.8594 - tn: 260.1875 - fn: 78.8438 - accuracy: 0.6963 - precision: 0.6854 - recall: 0.8078 - val_loss: 0.6597 - val_tp: 78.0000 - val_fp: 367.0000 - val_tn: 633.0000 - val_fn: 22.0000 - val_accuracy: 0.6464 - val_precision: 0.1753 - val_recall: 0.7800
Epoch 13/20
63/63 [==============================] - 6s 99ms/step - loss: 0.6989 - tp: 483.8438 - fp: 232.2188 - tn: 266.8281 - fn: 56.1094 - accuracy: 0.7253 - precision: 0.6895 - recall: 0.8748 - val_loss: 0.5315 - val_tp: 69.0000 - val_fp: 232.0000 - val_tn: 768.0000 - val_fn: 31.0000 - val_accuracy: 0.7609 - val_precision: 0.2292 - val_recall: 0.6900
Epoch 14/20
63/63 [==============================] - 6s 98ms/step - loss: 0.6369 - tp: 471.2656 - fp: 170.3750 - tn: 328.6719 - fn: 68.6875 - accuracy: 0.7725 - precision: 0.7628 - recall: 0.8367 - val_loss: 0.4832 - val_tp: 65.0000 - val_fp: 196.0000 - val_tn: 804.0000 - val_fn: 35.0000 - val_accuracy: 0.7900 - val_precision: 0.2490 - val_recall: 0.6500
Epoch 15/20
63/63 [==============================] - 6s 98ms/step - loss: 0.5847 - tp: 484.8438 - fp: 155.2656 - tn: 343.7812 - fn: 55.1094 - accuracy: 0.8016 - precision: 0.7773 - recall: 0.8783 - val_loss: 0.5749 - val_tp: 74.0000 - val_fp: 262.0000 - val_tn: 738.0000 - val_fn: 26.0000 - val_accuracy: 0.7382 - val_precision: 0.2202 - val_recall: 0.740023 - accuracy: 0.8038 - precision: 0
Epoch 16/20
63/63 [==============================] - 6s 98ms/step - loss: 0.4997 - tp: 490.9062 - fp: 134.4844 - tn: 364.5625 - fn: 49.0469 - accuracy: 0.8266 - precision: 0.7997 - recall: 0.8956 - val_loss: 0.4357 - val_tp: 62.0000 - val_fp: 163.0000 - val_tn: 837.0000 - val_fn: 38.0000 - val_accuracy: 0.8173 - val_precision: 0.2756 - val_recall: 0.6200: 61.5455 - tn: 196.2727 - fn: 29.6364 - accuracy: 0.8324 - precision: 0.8201 - r - ETA: 1s - loss: 0.4970 - tp: 355.6304 - fp: 91.8696 - tn: 266.7609 - fn: 37.7391 - accuracy: 0.8297 - prec
Epoch 17/20
63/63 [==============================] - 6s 98ms/step - loss: 0.4580 - tp: 490.7188 - fp: 111.7031 - tn: 387.3438 - fn: 49.2344 - accuracy: 0.8481 - precision: 0.8380 - recall: 0.8884 - val_loss: 0.5821 - val_tp: 73.0000 - val_fp: 264.0000 - val_tn: 736.0000 - val_fn: 27.0000 - val_accuracy: 0.7355 - val_precision: 0.2166 - val_recall: 0.7300
Epoch 18/20
63/63 [==============================] - 6s 98ms/step - loss: 0.4272 - tp: 505.8750 - fp: 109.4844 - tn: 389.5625 - fn: 34.0781 - accuracy: 0.8649 - precision: 0.8313 - recall: 0.9320 - val_loss: 0.6384 - val_tp: 75.0000 - val_fp: 261.0000 - val_tn: 739.0000 - val_fn: 25.0000 - val_accuracy: 0.7400 - val_precision: 0.2232 - val_recall: 0.7500
Epoch 19/20
63/63 [==============================] - 6s 98ms/step - loss: 0.3561 - tp: 505.4375 - fp: 89.5781 - tn: 409.4688 - fn: 34.5156 - accuracy: 0.8888 - precision: 0.8664 - recall: 0.9333 - val_loss: 0.8021 - val_tp: 82.0000 - val_fp: 363.0000 - val_tn: 637.0000 - val_fn: 18.0000 - val_accuracy: 0.6536 - val_precision: 0.1843 - val_recall: 0.8200
Epoch 20/20
63/63 [==============================] - 6s 98ms/step - loss: 0.3371 - tp: 511.7969 - fp: 87.0938 - tn: 411.9531 - fn: 28.1562 - accuracy: 0.8926 - precision: 0.8588 - recall: 0.9516 - val_loss: 0.7933 - val_tp: 79.0000 - val_fp: 304.0000 - val_tn: 696.0000 - val_fn: 21.0000 - val_accuracy: 0.7045 - val_precision: 0.2063 - val_recall: 0.7900: 0.8936 - precision: 0.8601 - recall:
Evaluation
Balanced Dataset
plot_loss(history_cat, "Cat Training")
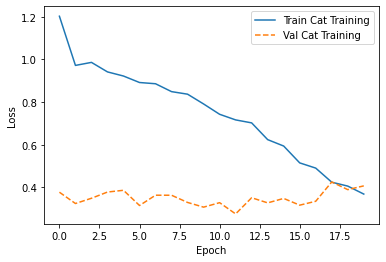
plot_loss(history_dog, "Dog Training")
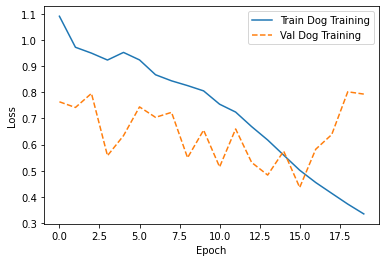
eval_cat_balanced = model_cat.evaluate(test_ds_balanced, batch_size=BATCH_SIZE, verbose=1)
eval_dog_balanced = model_dog.evaluate(test_ds_balanced, batch_size=BATCH_SIZE, verbose=1)
94/94 [==============================] - 11s 116ms/step - loss: 0.8130 - tp: 797.0000 - fp: 210.0000 - tn: 1290.0000 - fn: 703.0000 - accuracy: 0.6957 - precision: 0.7915 - recall: 0.5313
94/94 [==============================] - 6s 65ms/step - loss: 0.6802 - tp: 1142.0000 - fp: 433.0000 - tn: 1067.0000 - fn: 358.0000 - accuracy: 0.7363 - precision: 0.7251 - recall: 0.761379 - tp: 204.0000 - fp: 90.0000 - tn: 158.0000 - 5s 65ms/step - loss: 0.6767 - tp: 986.0000 - fp: 364.0000 - tn: 870.0000 - fn: 308.0000 - accuracy: 0.7342 - precisi
for name, value in zip(model_cat.metrics_names, eval_cat_balanced):
print(name, ': ', value)
loss : 0.812980055809021
tp : 797.0
fp : 210.0
tn : 1290.0
fn : 703.0
accuracy : 0.6956666707992554
precision : 0.7914597988128662
recall : 0.531333327293396
for name, value in zip(model_dog.metrics_names, eval_dog_balanced):
print(name, ': ', value)
loss : 0.6802101135253906
tp : 1142.0
fp : 433.0
tn : 1067.0
fn : 358.0
accuracy : 0.7363333106040955
precision : 0.725079357624054
recall : 0.7613333463668823
In the balanced one, the dog model has higher recall but lower precision. It also has higher accuracy, but that’s much closer between the models. Let’s look at the F1 scores.
cat_f1_balanced = calc_f1(eval_cat_balanced)
dog_f1_balanced = calc_f1(eval_dog_balanced)
print(f"Cat model F1 score: {round(cat_f1_balanced, 4)}")
print(f"Dog model F1 score: {round(dog_f1_balanced, 4)}")
Cat model F1 score: 0.6358
Dog model F1 score: 0.7428
The dog model has a higher F1 score. Now let’s look at the confusion matrices.
cat_preds_balanced = model_cat.predict(test_ds_balanced)
dog_preds_balanced = model_dog.predict(test_ds_balanced)
true_labels_balanced = tf.concat([y for x, y in test_ds_balanced], axis=0)
plot_cm(true_labels_balanced, cat_preds_balanced)
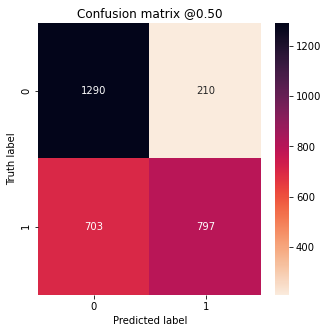
plot_cm(true_labels_balanced, dog_preds_balanced)
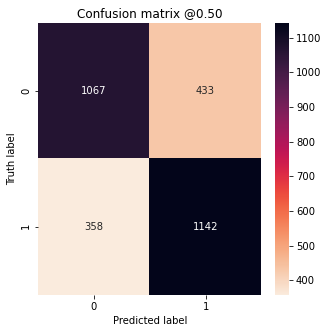
We can see that the dog model predicted more dogs and the cat model more cats, as expected.
Unbalanced Dataset
eval_cat_unbalanced = model_cat.evaluate(test_ds_unbalanced, batch_size=BATCH_SIZE, verbose=1)
eval_dog_unbalanced = model_dog.evaluate(test_ds_unbalanced, batch_size=BATCH_SIZE, verbose=1)
52/52 [==============================] - 16s 316ms/step - loss: 0.4111 - tp: 78.0000 - fp: 181.0000 - tn: 1319.0000 - fn: 72.0000 - accuracy: 0.8467 - precision: 0.3012 - recall: 0.5200
52/52 [==============================] - 3s 64ms/step - loss: 0.8164 - tp: 113.0000 - fp: 464.0000 - tn: 1036.0000 - fn: 37.0000 - accuracy: 0.6964 - precision: 0.1958 - recall: 0.7533
for name, value in zip(model_cat.metrics_names, eval_cat_unbalanced):
print(name, ': ', value)
loss : 0.4110898971557617
tp : 78.0
fp : 181.0
tn : 1319.0
fn : 72.0
accuracy : 0.846666693687439
precision : 0.3011583089828491
recall : 0.5199999809265137
for name, value in zip(model_dog.metrics_names, eval_dog_unbalanced):
print(name, ': ', value)
loss : 0.8164023756980896
tp : 113.0
fp : 464.0
tn : 1036.0
fn : 37.0
accuracy : 0.696363627910614
precision : 0.19584055244922638
recall : 0.753333330154419
In the unbalanced dataset, the dog model has higher recall but lower precision and this time much lower accuracy.
cat_f1_unbalanced = calc_f1(eval_cat_unbalanced)
dog_f1_unbalanced = calc_f1(eval_dog_unbalanced)
print(f"Cat model F1 score: {round(cat_f1_unbalanced, 4)}")
print(f"Dog model F1 score: {round(dog_f1_unbalanced, 4)}")
Cat model F1 score: 0.3814
Dog model F1 score: 0.3109
Conclusion
Immediately, we see that the performance of both models is far worse on the unbalanced dataset. But that’s how the real world data is going to be (in our pretend universe), so those are the metrics we need. Even more interesting, we see that while the dog model had the better score on the balanced test set, the cat model had the better one on the unbalanced dataset. However, the scores are quite close and given the dataset size, there’s a lot of uncertainty associated with these measurements. I would say only that this at least shows that this can happen.