The most frequently used evaluation metric for object detection is “Average Precision (AP)”. But, despite the attempts of well-intentioned researchers to create a single metric for comparing models, no single metric is the right one for all the cases. Thus the landscape of metrics has become filled with small variations on the idea of average precision. This post aims to clarify those variations.

Table of Contents

Precision and Recall

Before we can get into average precision, we’ll have to start with precision and recall. These are two of the most important metrics when evaluating the quality of a statistical model. They are particularly useful because they are both mathematically rigorous and have intuitive meanings. Imagine any model that classifies inputs are either “positive” or “negative”. Precision asks, “Out of all the times the model said the input was positive, what percentage were correct?” Recall asks “Out of all the times there was a positive, what percentage were found by the model?” Mathematically, they are calculated by looking at the number of true positives, false positives, and false negatives as follows:

\[\text{Precision}=\frac{TP}{TP+FP}\] \[\text{Recall}=\frac{TP}{TP+FN}\]

Note that the notion of “true negative” doesn’t exist for object detection. Every group of pixels that’s not an object would be a true negative so there are too many for the metric to be meaningful.

Thresholds and IoU

The notion of a true positive would seem fairly straightforward, but there are some nuances to discuss. For example, if a model predicts an object in an image and the bounding box is off by a few pixels, does it still count as a correct prediction? To determine that, we need a threshold for how much overlap to allow. The metric we use for this is known as the Intersection over Union, or IoU, score. It is defined as follows:

\[IoU(A,B) = \frac{A \cap B}{|A \cup B|}\]

The IoU score is also known as the Jaccard index.

Average Precision

Now let’s turn to average precision. Average precision was originally introduced in The PASCAL Visual Object Classes Challenge 2007 (Note that their website goes down all the time so there’s a mirror of it here). The term is exactly what it sounds like - the average precision, as defined above, of a model. What are we averaging? Well, by varying the threshold of the IoU score, we will produce different values of precision and recall. Thus the average precision is calculated by sampling the precision at a bunch of different thresholds and averaging them.

So, how do you calculate it? You have to change the threshold to keep increasing the recall, then find the precision at each point. Note that if you actually do this, the precision doesn’t decrease monotonically. That’s OK. You make the curve monotonic by setting the precision to be the highest value at that given recall or higher. This is because if you land at a bad spot you could always tweak the threshold to a value that’s going to give you higher precision and recall.

The way to do this in practice is to rank the detections by confidence and start with the highest confidence and see if that’s a true positive or false negative, then calculate the precision and recall based on that then plot the point. Then drop to the next highest confidence and repeat.

\[\text{AveragePrecision} = \int_0^1 p(r)dr\]

OK, so you know that “Average Precision”, or AP, is the area under the precision-recall curve. AP is between 0 and 100, with higher numbers better. Now let’s go one step further.

Multiclass classification

Many datasets have lots of objects. COCO, for example, has 80. To compare a model’s performance over every object category, the mean AP (mAP) averaged over all object categories is usually used. This means we find the AP value for each class and take the average. Note that mAP is not weighed by category frequency. If you have 1000 examples of a cat and an AP value of 0.9 and 10 examples of a dog and an AP value of 0.7, your mAP would be 0.8.

Multiple Thresholds

The final thing to introduce is the notion of multiple thresholds. Sometimes you want to know how a model performs at a variety of thresholds. In some cases, a rough idea of where an object is is all you need, so an IoU of 0.5 is fine. For others you need a precise localization, so you’ll use 0.95.

Instead of using a fixed IoU threshold, MS-COCO AP is averaged over multiple IoU thresholds between 0.5 (coarse localization) and 0.95 (near-perfect localization). So you get 10 different values. The mean of those values is the AP@[0.5:0.95]. This change of the metric has encouraged more accurate object localization and may be of great importance for some real-world applications. This is the most common metric for COCO evaluation and is written as mAP@(0.5:0.95).

Research Use Cases

A lot of papers will use both statistics. Here’s an example Faster R-CNN showing both:

metric

It’s showing mAP values at a threshold of 0.5, then the average of values at all thresholds from 0.5 to 0.95 in steps of 0.05.

Competition Examples

Pascal VOC vs COCO

Sometimes, different competitions use different values. For Pascal VOC, you’ll often see \(mAP@0.5\). For COCO, you’ll see \(mAP@[0.5:0.95]\). In general, the 0.5 IoU based mAP has then become the de facto metric for object detection problems for years.

Small, Medium, and Large Objects

Sometimes you’ll want to know the performance of models on objects of a specific size. That’s where \(AP_S\), \(AP_M\), and \(AP_L\) come in.

  • Small objects are defined as being between 0^2 and 32^2 pixels in area
  • Medium objects are defined as being between 32^2 and 96^2 pixels in area
  • Large objects are defined as being between 96^2 and 1e5^2 pixels in area

I’m not sure why there’s an upper limit to large objects, or what you would call an object above that.

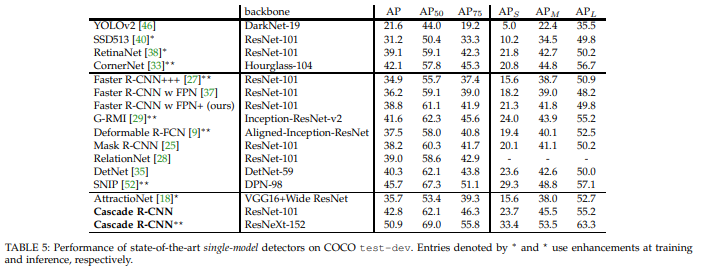
Here’s an example from Cascade R-CNN that shows \(AP\), \(AP_{50}\), and \(AP_{75}\). Then it shows AP values for small, medium, and large objects.

metric

  • Explain AP vs AP50

Very Small Objects

These thresholds of 0.5:0.95 are not ideal for all cases. For example, in geospatial analytics, the objects can be so small that these metrics are too strict. For example, if you have an object that is 5X5 pixels and the prediction is off to the side and above by one pixel, the IoU is bad. Your intersection is 16 pixels. Your union is 36 pixels. This gives an IoU of 16/36 = 0.44. So you’re only a pixel off but this would count as a miss. And it is very easy to be off by one pixel (especially if you consider label noise). For very small objects the threshold should be decreased.

Box vs Mask

Sometimes you’ll see APbbox or box AP or APbb. It’s the same as AP but they’re highlighting that it’s for bounding boxes to distinguish it from non-bounding box approaches, such as instance segmentation. Here’s an example from Mask R-CNN:

metric

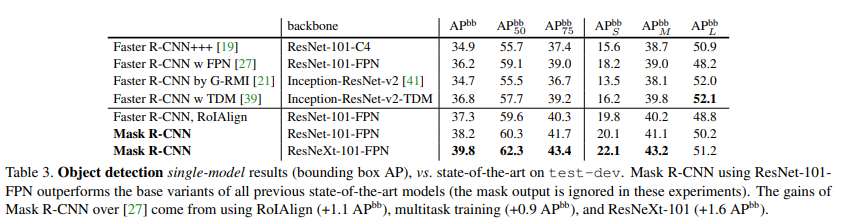
Sometimes you’ll also see key point scores.

F1

F1 scores are often better for production because you have an actual threshold value.

\[F1 = 2 \cdot \frac{\mathrm{precision} \cdot \mathrm{recall}}{ \mathrm{precision} + \mathrm{recall}}\]

Note that this is a generalization of FBeta

\[F_\beta = (1 + \beta^2) \cdot \frac{\mathrm{precision} \cdot \mathrm{recall}}{(\beta^2 \cdot \mathrm{precision}) + \mathrm{recall}}\]

Other Metrics

The question of which metrics to use isn’t a settled one. In fact, researchers are working on new approaches, like Localization Recall Precision, but they haven’t seen widespread adoption.