In the research paper Group Normalization by Yuxin Wu and Kaiming He, they introduce the idea of group normalization. They show that it can be applied very easily by including the necessary code in the paper. This post walks through the code behind group normalization.
import numpy as np
import tensorflow as tf
Let’s start with a random tensor. We’ll say that we’re somewhere inside the network and at this point we have images that are 112 X 112 and a depth of 16. We’ll also say we’re working with batches of size 64. Using the order N x C x H x W, our tensor would like like this:
tensor = np.random.random((64, 16, 112, 112))
Let’s look at it’s initial statistics.
def get_stats(tensor):
print("Object Type: ", type(tensor))
print("Shape: ", tensor.shape)
print("Mean: ", np.mean(tensor))
print("Standard Deviation: ", np.std(tensor))
print("Min: ", np.min(tensor))
print("Max: ", np.max(tensor))
get_stats(tensor)
Object Type: <class 'numpy.ndarray'>
Shape: (64, 16, 112, 112)
Mean: 0.5000566322329019
Standard Deviation: 0.288687413813454
Min: 1.2274301686154843e-08
Max: 0.9999997656106775
Let’s extract the different components from the tensor shape because we’ll need to manipulate them later on.
N, C, H, W = tensor.shape
To implement group norm, we’ll need a group size. This is the number of channels that we’re grouping together into a normalization group. This image from the Group Normalization paper illustrates that. In this illustration, the group size would be three, as you can see three highlighted blocks along the channel dimension.
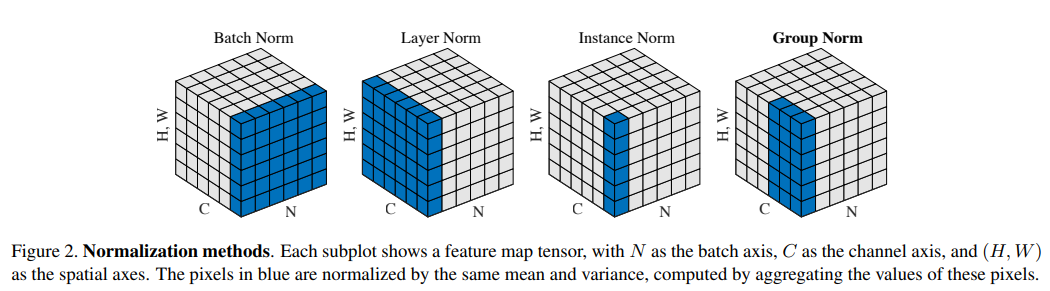
The number of input channels (16 in this case) needs to be evenly divisible by this number. We’ll choose 4 as our number.
G = 4
Now we need to reshape our tensor, adding a dimension for the group number. The first dimension is the batch size and remains unchanged, the second is the group size, the third is the number of groups (C // G), and the fourth and fifth are height and width, respectively.
tensor = tf.reshape(tensor, [N, G, C // G, H, W])
Let’s look at what those values are. Notice the shape now.
get_stats(tensor)
Object Type: <class 'tensorflow.python.framework.ops.EagerTensor'>
Shape: (64, 4, 4, 112, 112)
Mean: 0.5000566322329019
Standard Deviation: 0.288687413813454
Min: 1.2274301686154843e-08
Max: 0.9999997656106775
Note that now that we’ve used TensorFlow to reshape our tensor, it’s no longer a numpy array. Now it’s a TensorFlow EagerTensor.
Now we need to calculate the moments. The first moment of a probability distribution is the mean (expected value) and the second moment is the variance. Then we need to decide which axes to calculate the moments around. Each batch and group are going to have separate normalization parameters, so we don’t want to include those along the axes in the normalization. We want to calculate them along the width, height, and the number of channels in our group.
TensorFlow has a built in capability to calcuate moments, tf.nn.moments. It will return two objects with shape (in this case) 64, 4, 1, 1, 1. The first is the mean and the second is the variance.
mean, var = tf.nn.moments(tensor, [2, 3, 4], keepdims=True)
Now we use those values to normalize the group. The epsilon value is just there to avoid a divide by zero error. It’s 1e-5 in the original paper and in PyTorch, but 1e-3 in TensorFlow. The exact value shouldn’t matter.
tensor = (tensor-mean) / (var + 1e-5)
Then we put it back into the original shape.
tensor = tf.reshape(tensor, [N, C, H, W])
Then we include the scaling and shifting factors. Just like in batch norm, we multiply by the scale then add the shift factor. These are learnable parameters, but to start with you can set gamma to 1 and beta to 0 so they act as an identity function.
gamma = 1
beta = 0
tensor = tensor * gamma + beta
get_stats(tensor)
Object Type: <class 'tensorflow.python.framework.ops.EagerTensor'>
Shape: (64, 16, 112, 112)
Mean: 5.61705231647286e-17
Standard Deviation: 3.4636017539048107
Min: -6.078058331705886
Max: 6.075125228167952
You can look at the actual code as it’s written in TensorFlow. There’s a lot more going on there but the basics are the same.